三维旋转矩阵和刚体旋转(Object Rotation in 3D Space)
by lucainiaoge
如何描绘一个向量在三维世界中的旋转?如何描绘一个物体在三维世界中的旋转?
- 基础知识required:空间向量的概念
我们知道,在三维空间中,描绘一个三维列向量$\pmb{v}$逆时针绕着$z$轴旋转$\theta$角度,可以用这个矩阵来表示: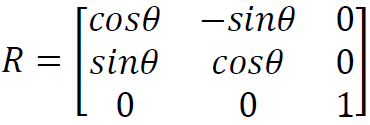
那么$Rv$就是旋转之后的向量了!
(如果不能理解,可以试试推导一下二维空间中向量绕原点旋转的矩阵)
同理,绕着x轴,y轴旋转的矩阵如下: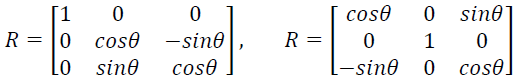
接下来:我们试着求一下三维空间中任何一个向量$\pmb{n_2}$绕着原点旋转到$z$轴方向的矩阵:肯定要经历两次二维旋转!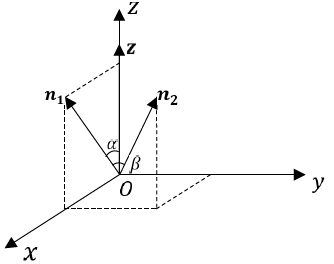
如上图:先绕$x轴$转到$xOz$平面,再绕$y轴$转到$z$方向。构造出来旋转矩阵: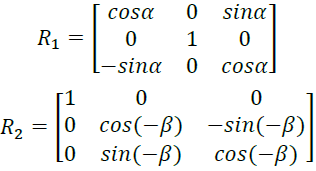
(上图中$\alpha \beta$ 的直角坐标计算公式就不给出了!)
那么$\pmb{n_2}=\pmb{R_1} \pmb{R_2} \pmb{e_z}$
我们令$\pmb{R_z}=\pmb{R_1R_2}$,即为将z单位向量$\pmb{e_z}$旋转到任意向量$\pmb{n}$的旋转矩阵(简记为z旋转矩阵)。$\pmb{R^{-1}}$即为将任意向量$\pmb{n}$旋转到$\pmb{e_z}$方向的旋转矩阵。
如何将任意向量$\pmb{n_1}$旋转到另一个任意向量$\pmb{n_2}$的方向?设$\pmb{n_1}$的z旋转矩阵为$\pmb{R_{z1}}$,$\pmb{n_2}$的z旋转矩阵为$\pmb{R_{z2}}$,那么先将$\pmb{n_1}$转到z轴,再将z轴转到$\pmb{n_2}$,得到$\pmb{n_2}=\pmb{R_{z2}}\pmb{R_{z1}^{-1}}\pmb{n_1}$
Rotation of Object
我们已知某个物体初始时刻的任意质点的位矢$\pmb{r}(x,y,z)$。现在,我们想描述这个物体绕着原点随便转动,转动的角度按球坐标系刻画,为:$xOy平面极角\beta$,$z轴极角\alpha$。对应的z旋转矩阵为$\pmb{R_{z}}$。
如果知道这个物体某个质点$\pmb{P}$位于$\pmb{e_{z}}$方向时其他质点相对于这个质点的位矢为$\pmb{\Delta r}=(\Delta x,\Delta y,\Delta z)$,那么$\pmb{R_{z}P}+\pmb{\Delta r}$即为刚体任意其他质点的方向了~
描述一个物体,只需要知道其一个位矢$\pmb{r}$(一般为质心),要旋转物体,只需要对$\pmb{r}$进行操作:$\pmb{R_{z}} \pmb{r}$,其余质点按照相对位置分配即可。
本文作者: lucainiaoge
本文链接: https://lucainiaoge.github.io.git/2019/10/02/rotation-in-3D-space/
版权声明: 本作品采用 Creative Commons authorship - noncommercial use - same way sharing 4.0 international license agreement 进行许可。转载请注明出处!

