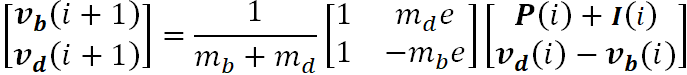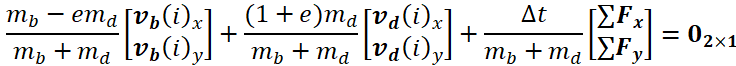2019-10-02

2019数模国赛B题解析Part2(Analysis of 2019CUMCM Question-B Part2)

by lucainiaoge

这篇文章讲解2019年数学建模国赛B题的求解历程。这是第二篇。

基础知识required：运动学和牛顿力学，空间向量的概念，最好有点反馈控制的知识（没有也行）

本文物理量如果无特殊说明一律采用国际单位制
若无法显示公式，或者出现[Math Processing Error]，请尝试shift+F5或者ctrl+shift+F5刷新页面

Restart: Operate in 3D World

上回书说道，为了解决前两问，我们搭建了~~逼真的物理引擎~~，然后建立了竖直方向施力的反馈机制。上一文章链接：2019数模国赛B题解析Part1(Analysis of 2019CUMCM Question-B Part1)

但是，我们怎么让我们的模型适用于三维世界？我们还有哪些没有做？捋了一遍，发现还差好多！具体总结如下：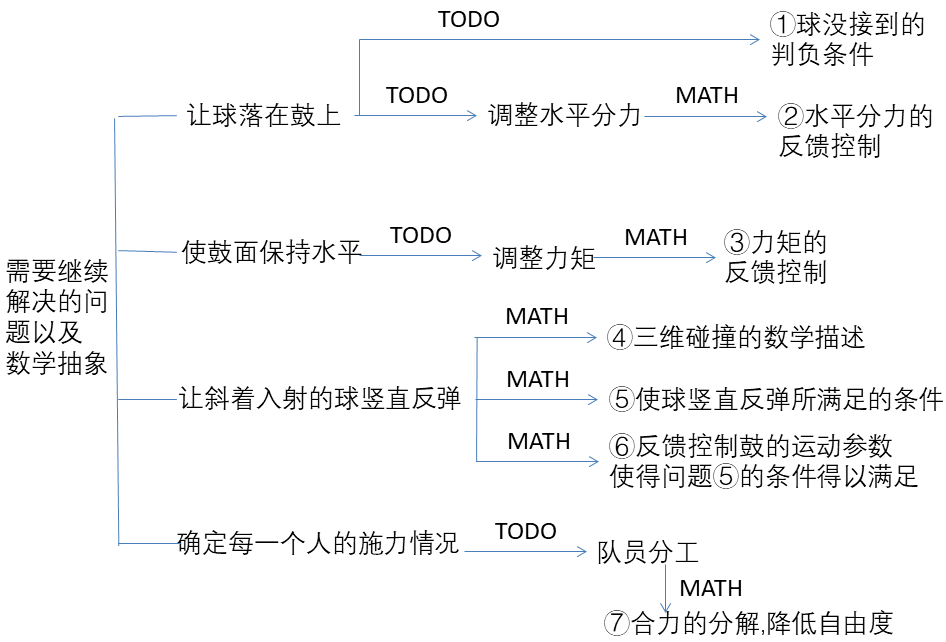

让我们逐(man)一(man)解决！

Solution: Get Feedback and Adjust

在这里依然使用反馈的思路，只不过不能是简单地画一个单调递减函数就能解决的问题了。这回，我们要按照控制论的思想实时进行控制了！

什么是控制论的思想？就是：首先，我们有一个目标的值，叫做期望值。假如我们想让$\Delta t$时间后，被控制物体的位置$\pmb{r}(t+\Delta t)$变到$\pmb{r_0}$，那么我们就说期望值为$\pmb{r_0}$。

在这里请允许我借用概率论中求期望的符号:$E[\pmb{r}(t+\Delta t)]=\pmb{r_0}$

请注意：这里的$E[·]$作用的对象是我们要调整的时变量，我们假定$E[·]$对于这些时变量的期望具有线性性质，这么认为的理由在后面会有解释。

那么接下来，我们就要竭尽所能达成这个期望。我们能干什么？当然是：调整力！牛顿力学的体系下，我们可以认为：力是改变物体运动状态的原因！

接下来，我是用PID（比例积分微分）的方法来进行控制。什么是PID？可以自行百度，这里只是一个名称罢了，代表一种方法，没必要知道工程上如何使用。实现这道题的要求，进行比例控制就够了。

如果仅使用比例控制，则$E[x]=K_p x$，$K_p$为比例系数。也就是下一次的输出量为期望值乘以一个系数。下文中，出现“求期望”字样，指的是获取目标量的期望值，不是统计学中的期望！

PID in problem ①&②

①好说，每次将要碰撞（球中心距离距鼓面距离等于球的半径）的时候进行一次判断，如果此时球在水平面的投影不落在鼓的投影内部，那么就判负。

主要讲如何实现②：控制拉力合力的水平分力，使鼓始终跟随球走。

力和位置，一个是二阶量，一个是零阶量，无法直接得出力的控制方程（就是决定下一时刻的输出量的计算式）。有一个办法：使用串级PID，不过这里我不打算采用这样的方法。

还有一个办法：我们连推两阶，就可以获取力的控制方程了。

下一时刻，鼓水平位置的期望值为球水平位置：
$E[\pmb{r_d}(i+1)]=\pmb{r_b(i)}$(注意，这里向量都是二维向量)
考虑运动方程$\pmb{r_d}(i+1)=\pmb{r_d}(i)+\pmb{v_d}(i)\Delta t$
由于实际世界是连续的，我们的迭代步长可以取得足够小，使得：$|\pmb{v_d}(i+1)-\pmb{v_d}(i)|<\epsilon$
所以运动方程还可写为：$\pmb{r_d}(i+1)=\pmb{r_d}(i)+\pmb{v_d}(i+1)\Delta t$

运动方程两边求期望得到：$E[\pmb{v_d}(i+1)]=(E[\pmb{r_d}(i+1)]-\pmb{r_d}(i))/\Delta t=(\pmb{r_b}(i)-\pmb{r_d}(i))/\Delta t$
记$\pmb{r_{db}}(i)=(\pmb{r_b}(i)-\pmb{r_d}(i))$
则有$E[\pmb{v_d}(i+1)]=\pmb{r_{db}}(i)/\Delta t$
仅使用PID比例控制，则可以拆掉期望运算$\pmb{v_d}(i+1)=\pmb{K_{pv}}\pmb{r_{db}}(i)/\Delta t$
其中：$\pmb{K_{pv}}=diag(k_{vx},k_{vy})$
又根据冲量定理，$\pmb{v_d}(i+1)=\pmb{v_d}(i)+\pmb{F_{xy}}(i)\Delta t/m_d$
结合以上式子，经过简单代入和移项，可以推出：

$\pmb{F_{xy}}(i)=\pmb{K_{pv}}\pmb{r_{db}}(i)m_d/(\Delta t)^2-\pmb{v_d}(i)m_d/\Delta t $
这就是我们想要的控制方程，按照这个式子设置此时的合力即可使得鼓的水平位置趋向于球的水平位置！

PID in problem ③

③的目的是：让鼓始终保持水平。为什么要让鼓保持水平？一个原因是让球更容易被接到；还有一个原因就是减少转动防止力的不均匀性使得鼓过不了多久就转翻了。
对于力矩的推导相似，但是更复杂。具体呢：看下面吧！

我们期望鼓的法向量$\pmb{n}(i+1)$为$z单位向量\pmb{e_z}$，即$E[\pmb{n}(i+1)]=\pmb{e_z}$
根据转动定理和连续性，$\pmb{n}(i+1)=\pmb{n}(i)+\pmb{\omega}(i+1)\times\pmb{n}(i)\Delta t$
两边求期望得到$E[\pmb{\omega}(i+1)]\times\pmb{n}(i)\Delta t=E[\pmb{n}(i+1)]-\pmb{n}(i)$
代入$E[\pmb{n}(i+1)]=\pmb{e_z}$得到$E[\pmb{\omega}(i+1)]\times\pmb{n}(i)\Delta t=\pmb{e_z}-\pmb{n}(i)$
我们仅使用比例控制PID，那么可以继续拆掉期望运算，得到：
$\pmb{\omega}(i+1)\times\pmb{n}(i)\Delta t=\pmb{K_{pr}}(\pmb{e_z}-\pmb{n}(i))$
其中，$\pmb{K_{pr}}=diag(k_{rx},k_{ry},k_{rz})$
列出动力学公式$J\pmb{\omega}(i+1)=J\pmb{\omega}(i)+\pmb{M}(i)\Delta t$
将动力学公式两边同时叉乘$\pmb{n}(i)$，结合已得到的式子，推出
$\pmb{M}(i)\times\pmb{n}(i)\Delta t=J\pmb{K_{pr}}(\pmb{e_z}-\pmb{n}(i))/\Delta t-J\pmb{\omega}(i)\times\pmb{n}(i)$
我们最终要得到$\pmb{M}(i)$<所以把这个向量积方程解出来就好了。这个方程怎么解？
我们先把和设定值$\pmb{M}(i)$无关的已知量（即时刻$i$的运动参量）挪到一边去，
令$\pmb{S}(i)=J[\pmb{K_{pr}}(\pmb{e_z}-\pmb{n}(i))/\Delta t-\pmb{\omega}(i)\times\pmb{n}(i)]/\Delta t$
那么这个方程就写成了$\pmb{M}(i)\times\pmb{n}(i)=\pmb{S}(i)$
求解过程如下图

最终得到：

$\pmb{M}(i)=diag(-S_y(i)/n_z(i),S_x(i)/n_z(i),0)$
这就是我们想要的力矩的控制方程，按照此式子迭代可以使得鼓始终保持水平

Problem ④&⑤

问题一个个解决，一半多的理论问题已经被搞定了！那么，三维碰撞怎么描绘？如何刻画使球竖直弹回的条件？

Describe 3D Collision

先解决碰撞的迭代公式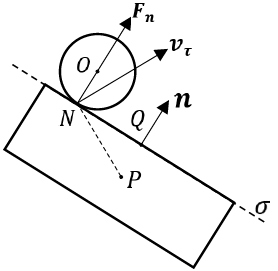

上图是碰撞瞬间部分物理量的示意图。我们需要研究N点两个物体的速度。这涉及到了：鼓在N点的线速度(质心速度和转动线速度之和)、鼓的转动角速度、碰撞点的位置、球的质心速度(之前假设不考虑球的自转)。让我们一一列方程！
设鼓的厚度为$h$，球的半径为$R$，用单一字母代表原点到该字母表示点的向量，那么有
$\pmb{PQ}=h\pmb{n}/2$,$\pmb{N}=\pmb{O}-h\pmb{n}/2$,$\pmb{Q}=\pmb{P}+\pmb{PQ}$
我们知道$平面\sigma:n_x(x-x_Q)+n_y(y-y_Q)+n_z(z-z_Q)=0$
其中$n_x,n_y,n_z$为鼓面单位法向量的分量
那么球到鼓面的距离为$d_{ON}=|n_x(x_O-x_Q)+n_y(y_O-y_Q)+n_z(z_O-z_Q)|$
每次迭代判断一次$d_{ON}\le R?$，如果成立则对碰撞进行迭代：
设此时鼓的质心速度为$\pmb{v_d}$，鼓的角速度为$\pmb{\omega}$，$N$点处鼓的旋转线速度为$\pmb{v_{\tau}}$，N点鼓的质点速度为$\pmb{v_{N}}$，球的质心速度为$\pmb{v_d}$，那么我们有：
$\pmb{v_{\tau}}=\pmb{\omega}\times\pmb{PN}$
$\pmb{v_{N}}=\pmb{v_d}+\pmb{v_{\tau}}$
下面，列写动力学方程更新下一时刻鼓和球的运动参量：
对物体列冲量定理和碰撞系数定义式
$\pmb{P}(i)=m_{b} \pmb{v_b}(i)+m_{d} \pmb{v_d}(i) $（前一时刻动量）
$\pmb{P}(i+1)=m_{b} \pmb{v_b}(i+1)+m_{d} \pmb{v_d}(i+1) $（后一时刻动量）
$I(i)=\sum \pmb{F}(i) \Delta t-\left(m_{b}+m_{d}\right) g \Delta t \pmb{e_z} $（外力冲量）
$\pmb{P}(i)+\pmb{I}(i)=\pmb{P}(i+1) $（冲量定理）
$e\left[\pmb{v_b}(i+1)-\pmb{v_d}(i+1)\right]=\pmb{v_d}(i)-\pmb{v_b}(i) $（碰撞系数定义）

上面$\pmb{\sum F}$为队员拉力的合力。
可以求得下一时刻二者的质心速度

对系统列角动量守恒得到
$J\pmb{\omega}(i)+\pmb{PO}\times m_b\pmb{v_b}(i)=J\pmb{\omega_d}(i+1)+\pmb{PO}\times m_b\pmb{v_b}(i+1)$
整理得到下一时刻鼓的角速度

$\pmb{\omega}(i+1)=\pmb{\omega}(i)+\pmb{PO}\times m_b(\pmb{v_b}(i)-\pmb{v_b}(i+1))$

Describe the Condition in ⑤

下面，我们需要探究碰撞瞬间满足什么条件，就可以将球竖直弹回。
如果下一时刻球竖直弹回，那么一定有：
$\pmb{v_b}(i+1)\times\pmb{e_z}=0$
根据上一部分推出的鼓质心速度$\pmb{v_d}(i+1)$的计算公式，忽略重力影响，得到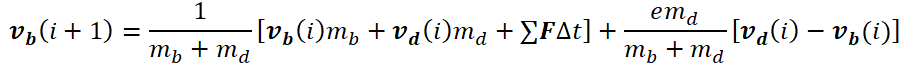

式子两边同时叉乘$\pmb{e_z}$并移项化简，得到：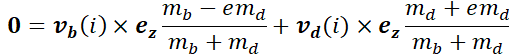

写成分量形式并运算向量积，得到：

这就是让球竖直弹回应该满足的条件。可以发现，如果不考虑碰撞过程中摩擦等情况，仅调用碰撞系数，球在下一时刻的弹回方向仅由鼓和球的水平质心速度决定，而且二者速度反向共线。

Problem ⑥

将上一部分推导的条件写成二维向量的向量表达式：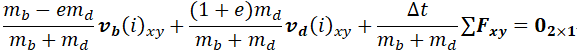

下面推导省去脚标$xy$，向量都是二维向量，$水平合力\pmb{F_{xy}}=\pmb{\sum T}$。
将此式子中的$ \pmb{v_d}(i)$作为下一时刻鼓速度$\pmb{v_d}(i+1)$的参考值。移项，可以获得：
$E[\pmb{v_d}(i+1)]=-(\frac{\pmb{\sum T(i)}-(m_b+m_d)g\pmb{e_z}}{(1+e)m_d}\Delta t + \frac{m_b-em_d}{(1+e)m_d}\pmb{v_b}(i))$
仅采用比例控制PID，则可以拆掉期望运算：
$\pmb{v_d}(i+1)=-\pmb{K_{pf}}(\frac{\pmb{\sum T(i)}-(m_b+m_d)g\pmb{e_z}}{(1+e)m_d}\Delta t + \frac{m_b-em_d}{(1+e)m_d}\pmb{v_b}(i))$
其中$\pmb{K_{pf}}=diag(k_{fx},k_{fy})$
结合冲量定理：$m_d\pmb{v_d}(i+1)-m_d\pmb{v_d}(i)=\pmb{\sum T(i)}\Delta t$
令$\lambda=(em_d-m_b)/\Delta t$，再参考连续性并化简上式可以得到：

$\pmb{F_{xy}}(i)=\pmb{\sum T(i)}=diag(\frac{\lambda k_{fx}-1}{1+k_{fx}},\frac{\lambda k_{fy}-1}{1+k_{fy}})\pmb{v_b}(i)$
这就是迎接球使其竖直弹回需要设定的下一时刻水平合力迭代公式
细心的小伙伴会发现：这个式子和之前问题②的迭代式子打架了，不过没关系，我们使用分段PID，在判断球快要碰撞时才采用此表达式。

Results: 3D movement

先上效果图：
如何实现的？之前我们的准备工作已经十分充足了！话不多说，现在只需要把迭代公式列一遍：

Section 0: get several values
$d_{ON}=|n_x(x_O-x_Q)+n_y(y_O-y_Q)+n_z(z_O-z_Q)|$ (球到鼓面的距离)
set $\pmb{K_{pv}},\pmb{K_{pr}},\pmb{K_{pf}},\epsilon_d,\epsilon_v,\epsilon_{collide}$

Section 1: set $\pmb{M}(i),\pmb{F}(i), status \quad X$

角动量设置
$\pmb{S}(i)=J[\pmb{K_{pr}}(\pmb{e_z}-\pmb{n}(i))/\Delta t-\pmb{\omega}(i)\times\pmb{n}(i)]/\Delta t$
$\pmb{M}(i)=diag(-S_y(i)/n_z(i),S_x(i)/n_z(i),0)$

水平合力设置
$if \quad d_{ON}>\epsilon_d$ ……(距离较远，鼓追球)
$\quad\pmb{F_{xy}}(i)=\pmb{K_{pv}}\pmb{r_{db}}(i)m_d/(\Delta t)^2-\pmb{v_d}(i)m_d/\Delta t $ ……(二维向量)
$else$ ……(距离较近，鼓迎球)
$\quad\lambda=(em_d-m_b)/\Delta t$
$\quad\pmb{F_{xy}}(i)=diag(\frac{\lambda k_{fx}-1}{1+k_{fx}},\frac{\lambda k_{fy}-1}{1+k_{fy}})\pmb{v_b}(i)$…… (二维向量)

竖直合力设置
$F_z(i)=min(F_X(i),T_{lim}(z_d(i)))$,$F_X(i)\in \lbrace F_I,F_{II},F_{III},F_{IV} \rbrace$

根据第一问的状态机更新状态X(此处略去)

Section 2: physics system

rotation
$\pmb{\omega}(i+1)=\pmb{\omega}(i)+\pmb{M}(i)\Delta t/J$……(转动定理)
$\pmb{\Delta n}(i)=\pmb{n(i)}\times\pmb{\omega}(i)\Delta t$……(角速度造成的法向量瞬时变化量)
$\pmb{n}(i+1)=\pmb{n}(i)+\pmb{\Delta n}(i)$……(更新法向量)
$\pmb{n}(i+1)=\pmb{n}(i+1)/ | \pmb{n}(i+1) |$……(归一化消除长度误差)
$\pmb{R_k^o}(i+1)=\pmb{R}(i+1)\pmb{R_k^o}(1)$……(更新鼓的径向,R为旋转矩阵)

translation
drum：
$\pmb{f_{d_{air}}}(i) = 0.5 C_d \rho S_d \pmb{v_d}(i) |\pmb{v_d}(i)|$
$m_d \pmb{v_d}(i+1) = (-m_d g\pmb{e_z} + \rho V_d g\pmb{e_z} - \pmb{f_{d_{air}}}(i) + \pmb{F}(i))\Delta t + m_d \pmb{v_d(i)}$
$\pmb{r_d}(i+1) = \pmb{r_d}(i) + \pmb{v_d}(i)\Delta t$
ball：
$\pmb{f_{b_{air}}}(i) = 0.5 C_b \rho S_b \pmb{v_b}(i) |\pmb{v_b}(i)|$
$m_b \pmb{v_b}(i+1) = (-m_b g\pmb{e_z} + \rho V_b g\pmb{e_z} - \pmb{f_{b_{air}}}(i) + m_b \pmb{v_b(i)}$.
$\pmb{r_b}(i+1) = \pmb{r_b}(i) + \pmb{v_b}(i)\Delta t$

collision
$if \quad d_{ON}<\epsilon_{collide}$
$\quad\pmb{P}(i)=m_{b} \pmb{v_b}(i)+m_{d} \pmb{v_d}(i) $
$\quad I(i)=\pmb{F}(i) \Delta t-\left(m_{b}+m_{d}\right) g \Delta t \pmb{e_z} $
$\quad$
$\quad\pmb{\omega}(i+1)=\pmb{\omega}(i)+\pmb{r_{db}}(i)\times m_b(\pmb{v_b}(i)-\pmb{v_b}(i+1))$

Section 3: judge system
$if \quad d_{ON}<\epsilon_{collide}$……(接不到球)
$\quad if \quad (x_d-x_b)^2+(y_d-y_b)^2>R_d^2$……(简单化处理)
$\quad\quad fail=2$
$if \quad v_b(i)<\epsilon_{v}$……(球达到最高)
$\quad if \quad d_{ON}<0.4$……(球太低的判负)
$\quad\quad fail=1$

Implementation: solve Q4 partially

Q4: 当鼓面发生倾斜时，球跳动方向不再竖直，于是需要队员调整拉绳策略。假设人数为10，绳长为2m，球的反弹高度为60cm，相对于竖直方向产生1度的倾斜角度，且倾斜方向在水平面的投影指向某两位队员之间，与这两位队员的夹角之比为1:2。为了将球调整为竖直状态弹跳，请给出在可精确控制条件下所有队员的发力时机及力度，并分析在现实情形中这种调整策略的实施效果。

初始条件，按照我们的解读刻画如下：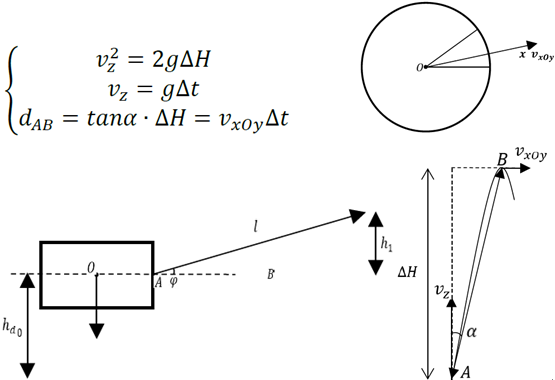

$\pmb{r_b}(1) =\left(\cos \left(\left(\frac{2 \pi}{N}\right)(k-1)+\frac{2 \pi}{3 N}\right) x, \sin \left(\left(\frac{2 \pi}{N}\right)(k-1)+\frac{2 \pi}{3 N}\right) x, \Delta H\right)$
$\pmb{v_b}(1) =\left(\cos \left(\left(\frac{2 \pi}{N}\right)(k-1)+\frac{2 \pi}{3 N}\right) v_{x O y}, \sin \left(\left(\frac{2 \pi}{N}\right)(k-1)+\frac{2 \pi}{3 N}\right) v_{x O y}, 0\right)$

代入初始条件，依然按照目标规划搜索三组比例系数，z方向直接调用第一问的最优结果(我们跑了很多次，由于搜索时间实在太长，每次都没跑完，所以在这里只取一个有代表性的来演示，论文中用的另一个结果)，得到第四问的决策结果和游戏过程：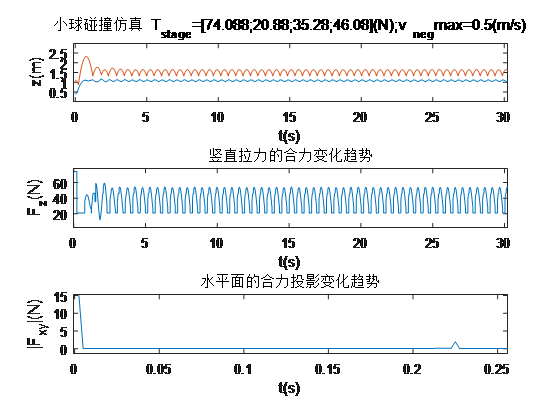

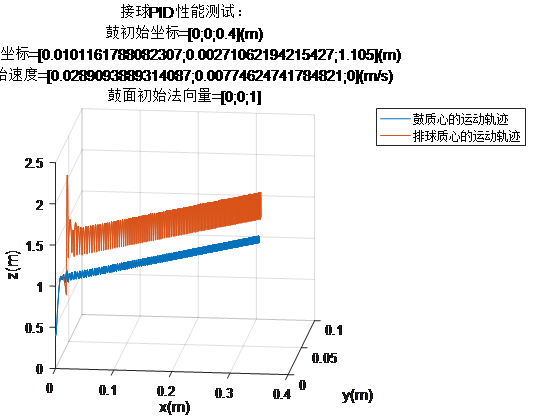
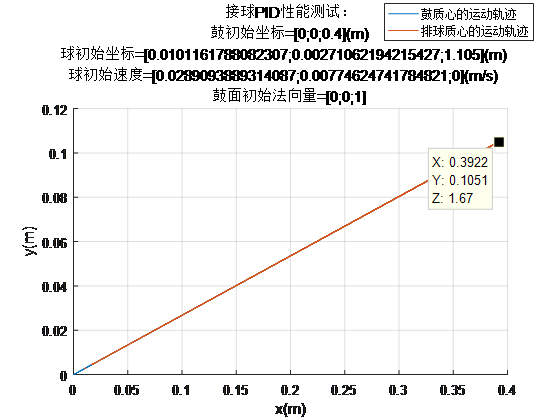
Complete the system

Solve problem ⑦

这个问题是本队翔哥解决的，在这里直接贴出来原汁原味的总结：

按照这个规则分解以后，代入问题4的初始条件，出来结果是这样子：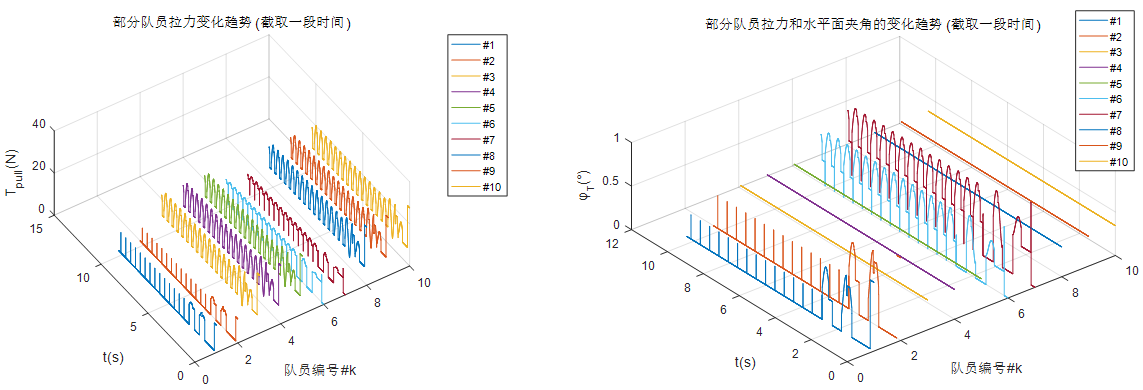

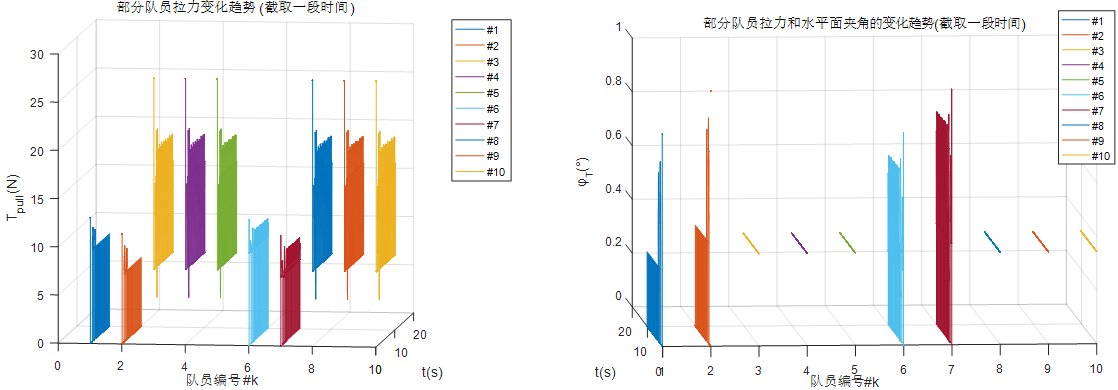
System Summary and Robustness Analysis

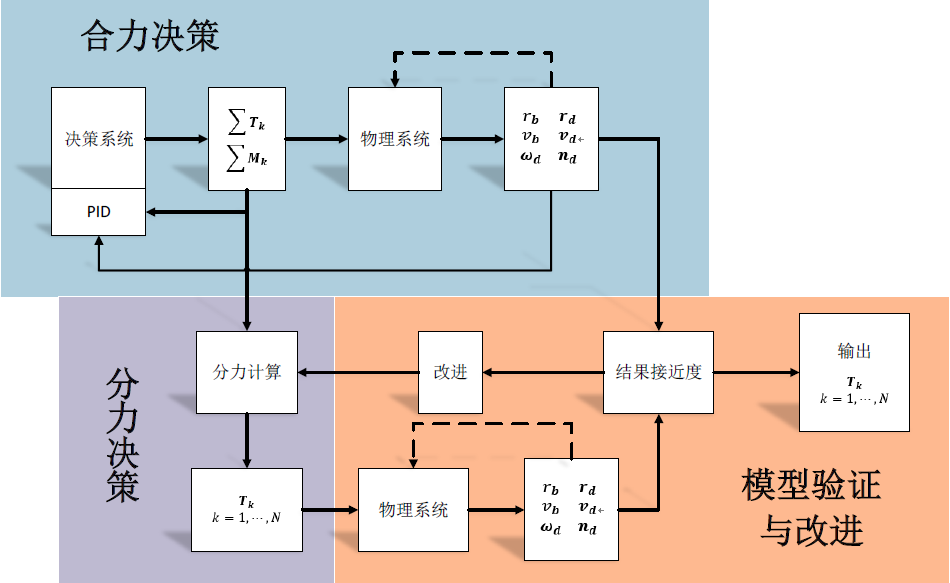
可以看到，大部分我们已经做完，就差最后一个验证了。计算接近度，我们使用的是相关系数。将上面搞出来的分力合成以后再次代入系统，发现：原来设定25000步，运行了11584步就输掉了。大概是因为重新合成的力没有引入反馈吧，误差会累计。不过结果已经相当不错了。
计算一下接近度（标注part的是只算了11584步的接近度）

发现即使力非常接近（都是1），运行轨迹也不是很接近。反馈的重要性可见一斑了。

一个遗憾：时间和能力有限，我们没有做分力代入系统的实时反馈以及考虑了力矩的合力分解。

啊写了好多！鲁棒性分析就贴图好了。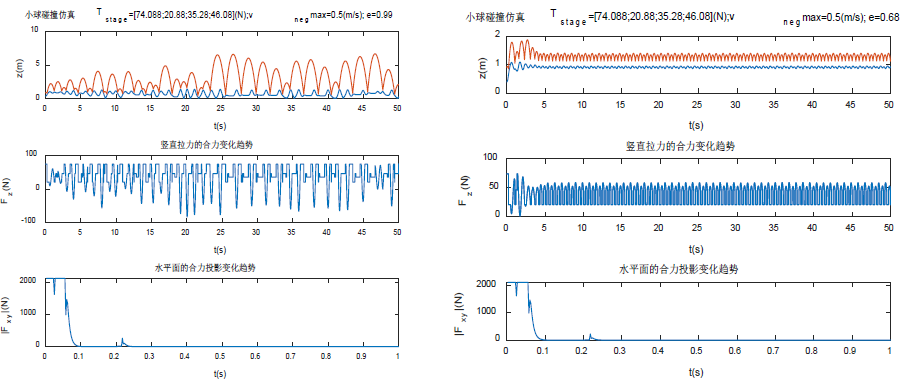

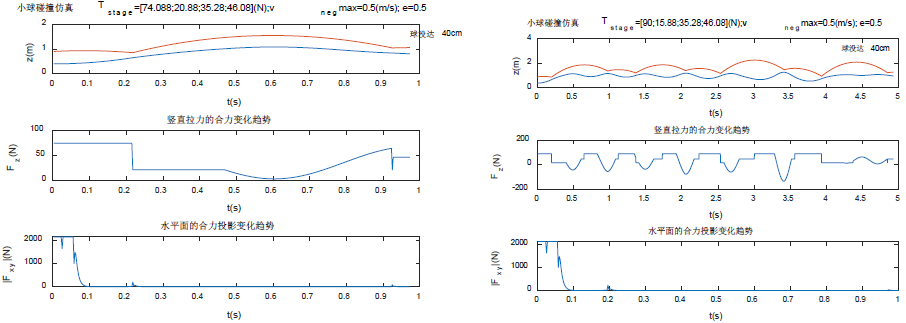
结果是：系统至少可以支持碰撞系数0.68<e<0.99的变化，在此区间内可以无限颠球。

At last

先写到这里吧，期间有许多细节也略过了，毕竟要总结的东西特别多，要抓住重点。

总觉得这次数学建模以后，~~我就可以去游戏公司开发3D游戏了！~~
其实自己写出仿真程序还是很爽的，体验了一把决定论哲学下的上帝视角！今后用到控制、用到三维世界描述的时候，也会更加得心应手。

数学建模还是很占精力的，尤其是当你不是为了划水得奖而是认认真真研究问题的时候。不过闹了半天，我也没有用上什么特别先进特别现代的算法，也没用上什么近代的数学知识。不过也不要好高骛远，慢慢成长慢慢来，时间可以填补知识空白。

祝大家学业有成，参加数模的小伙伴遇到自己心仪的问题，有志于科研的小伙伴遇到自己心仪的课题（祝我自己）！

2019数学建模系列传送门

本文作者： lucainiaoge
本文链接： https://lucainiaoge.github.io.git/2019/10/02/math-modling-2019CUMCM-answer-2/
版权声明： 本作品采用 Creative Commons authorship - noncommercial use - same way sharing 4.0 international license agreement 进行许可。转载请注明出处！

Welcome to my little world