2019-09-29

2019数模国赛B题解析Part1(Analysis of 2019CUMCM Question-B Part1)

by lucainiaoge

这篇文章讲解2019年数学建模国赛B题的求解历程。

基础知识required：运动学和牛顿力学，空间向量的概念

本文物理量如果无特殊说明一律采用国际单位制
若无法显示公式，或者出现[Math Processing Error]，请尝试shift+F5或者ctrl+shift+F5刷新页面

First Sight: Discovering and Creating

问题链接：

全国大学生数学建模大赛官网http://www.mcm.edu.cn/，进去点击“赛题与评奖”，即可获取赛题

我们做的是B题，同心鼓那个。起初我觉得这题很没劲，但做起来以后才觉得有意思。数学建模心路历程和经历已经写过了，可以看我博客的这套文章：2019数学建模国赛总结 Part 1

解决第一问：

Q1. 在理想状态下，每个人都可以精确控制用力方向、时机和力度，试讨论这种情形下团队的最佳协作策略，并给出该策略下的颠球高度。

Solve by simulation

我们拿到问题，首先考虑：我们要输出什么样子的结果？
我们要输出“最佳协作策略”。既然要建模，一定要定量，那么这个策略也是定量的。想：协作需要确定什么量？以人为单位，每个人需要通过绳子提供拉力，拉力包含夹角和方向，同时也包含随时间变化的信息（毕竟游戏是一个过程）。

怎么刻画这些量？$\varphi_k - t \quad curve \quad and \quad \textbf{F}_k - t \quad curve$

$\varphi_k$是每个人施力夹角，$\textbf{F}_k$是每个人施力的大小

有了这个思路，我们就要确定这个有关每个人施力随时间变化的函数了。这个函数的目的：使得游戏得分最高。即：将函数输入游戏，游戏输出得分结果，我们要这么样的函数使得结果最优——优化问题。那么我们又要开始想：游戏如何输入这个函数？我们要构建游戏的真实过程！

到此为止，我们其实已经进入正题上了——构建游戏的过程。说白了：物理仿真系统！

仿真系统的构建，我们使用MATLAB，后面也一直在用MATLAB。我首先写了一个最简单的仿真系统——小球与地碰撞反弹的系统。

我们能参考的是什么？运动学方程，牛顿运动定律，碰撞定理。

以最简单的反弹系统为例，我们有这么几个微分方程：
$\frac{dy(t)}{dt} = v(t)$
$\frac{dv(t)}{dt} = g$
$v(t+\Delta t)=-ev(t) \quad when \quad y(t)<\epsilon$, e为碰撞系数

我们要做的是将其以时间步长$\Delta t$离散化以适应MATLAB仿真：

$y(i+1)-y(i) = v(t) \Delta t$
$v(i+1)-v(i) = g \Delta t$
$v(i+1)=-ev(i) \quad when \quad y(i)<\epsilon$

好的，接下来就要代码实现了。其实，上面已经给出了迭代公式。离散化其实是对实际世界的近似。实际世界一切物理现象的发生可以看成是同时的，不会出现“上帝先确定某物体的加速度，再确定它的速度，最后确定它的位置”这种情况（至少用微分方程求解是这样的）。但我们迭代时候，就产生了这样的问题：我们有很多迭代公式，先迭代哪个？

如果我们要求解差分方程组，也不存在这个问题，毕竟求解差分方程和求解微分方程是一个套路，最后得出的解与我们先解出哪个方程无关。可是迭代的话，我们先算谁后算谁，有一个因果性。我们一般按照高阶(eg:加速度，速度)到低阶(eg:速度，位置)的顺序来迭代。
实例代码如下：

for i=1:max_step
   t=t_step*i;
   v(i+1)=-g*t_step+v(i);
   y(i+1)=v(i-1)*t_step+y(i);
   if(y(i)<eps)
       v(i+1)=-v(i)*0.998;
   end
end

运行这个代码，可以得到这样的过程（横轴是时间）：

Creat 1D Physical Simulation System

我们其实完成了历史性的一步：构建了一个物理仿真系统。接下来，就是将其应用到题目中了。

题目第一问对实际施力情况可以做理想化处理。理想到什么程度？我们的把握是：让每个均匀站立的人可以做到对称施力——竖直分力相等，水平分力也相等使得八个人水平合力为0。那么，我们只需获取竖直方向合力，结合任何时刻人的高度和鼓的高度，即可得到每个人的分力以及力的夹角了。现在，我们的任务就是：设定每个时刻的竖直合力。

我们要考虑两个物体的运动。模型较为简单，迭代求解甚至可以考虑空气阻力、浮力等因素（不用获取解析形式，是数值方法的一大优点，这样可以使得我们考虑很多通过解析方法很难刻画的因素）。在我们直接列离散化之后的方程如下(为节省篇幅，一些明显易求得的物理量[例如截面积和体积]在这里不加以计算，仅做符号说明)：

符号说明：
- 脚标”d”代表”drum”，即“鼓”；脚标”b”代表”ball”，即“球”；
- “C”是空气阻力系数，对于球而言$C_b = 0.5$，对于圆柱而言$C_d = 0.73$
- “V”代表体积，”S”代表截面积，”$F_z$”代表队员的竖直合力，”$\rho$”代表空气密度，”m”表示质量
- 指标$i$代表迭代变量（即时间），$\Delta t$为迭代步长

$f_{d_{air}}(i) = 0.5 C_d \rho S_d v_d(i) |v_d(i)|$……(鼓的空气阻力)
$f_{b_{air}}(i) = 0.5 C_b \rho S_b v_b(i) |v_b(i)|$……(球的空气阻力)
$m_d v_d(i+1) = (-m_d g + \rho V_d g - f_{d_{air}}(i) + F_z(i))\Delta t + m_d v_d(i)$……(鼓的速度迭代公式)
$m_b v_b(i+1) = (-m_b g + \rho V_b g - f_{b_{air}}(i))\Delta t + m_b v_b(i)$……(球的速度迭代公式)
$z_d(i+1) = z_d(i) + v_d(i)\Delta t$……(鼓的位置迭代公式)
$z_b(i+1) = z_b(i) + v_b(i)\Delta t$……(球的位置迭代公式)
$if \quad z_b(i)-z_d(i)<\epsilon \quad :$(碰撞迭代公式)

碰撞的迭代公式的推导由来如下图所示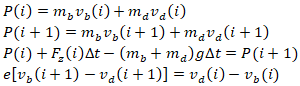

其中P代表冲量，这几个式子是列了冲量定理和碰撞系数e的定义式。

How to Set $F_z(i)$

上面的物理模型想要运行，必须实时输入$F_z(i)$，所以我们需要构建一个确定$F_z(i)$的系统。想了半天，憋出来一个想法：使用状态机并引入反馈。

什么是状态机？就是设置决策者在不同情况下进入不同的状态，不同的状态下做出不同的决策。这里，我们设置了这么几种状态：

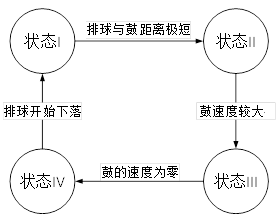
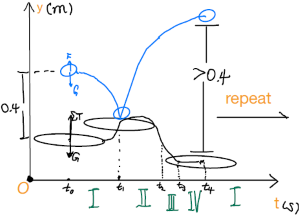
在不同状态下，设定不同的$F_z(i)$值，即：$F_z(i)\in \lbrace F_I,F_{II},F_{III},F_{IV} \rbrace$，每次迭代都根据目前状态设置$F_z(i)$即可。

我们探索了几个$F_z(i)$的值，比如$[F_I,F_{II},F_{III},F_{IV}]=[(g+6)m_d,0,gm_d,(g+3)m_d]$，设置鼓向下运动最大速度为0.6m/s，按照上述图片的状态转换规则进行迭代，会得到这样的结果(在这里我也加入了和地面碰撞反弹的判断)(红线是球的运动轨迹，蓝线是鼓面的运动轨迹，碰撞判断时没有考虑球的大小)：

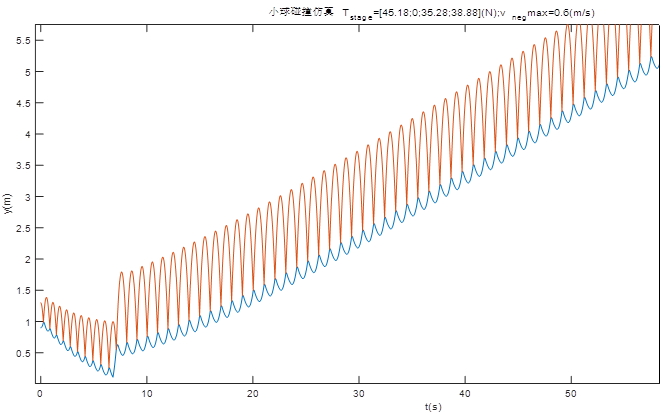
会发现，要不就往下掉，要不就越飞越高，没有实现稳定地控制。怎么让它稳定？我们想到了引入负反馈！也就是，鼓太高的时候，就减少向上的力使鼓保持在下面。

反馈很简单，设置一个分段函数$T_{lim}(y)$如下：

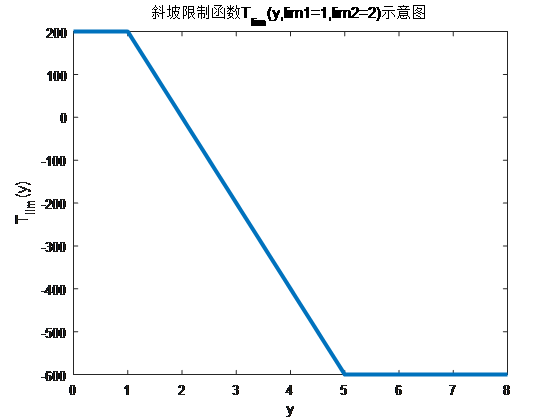
每次迭代按照状态设置完参考竖直力之后，按照这个函数限制一下$F_z(i)$(这个函数是力的上限，如果设定值大于$T_{lim}(z(i))$，就将$F_z(i)$设置为$T_{lim}(z(i))$)。于是得到了令人满意的结果：

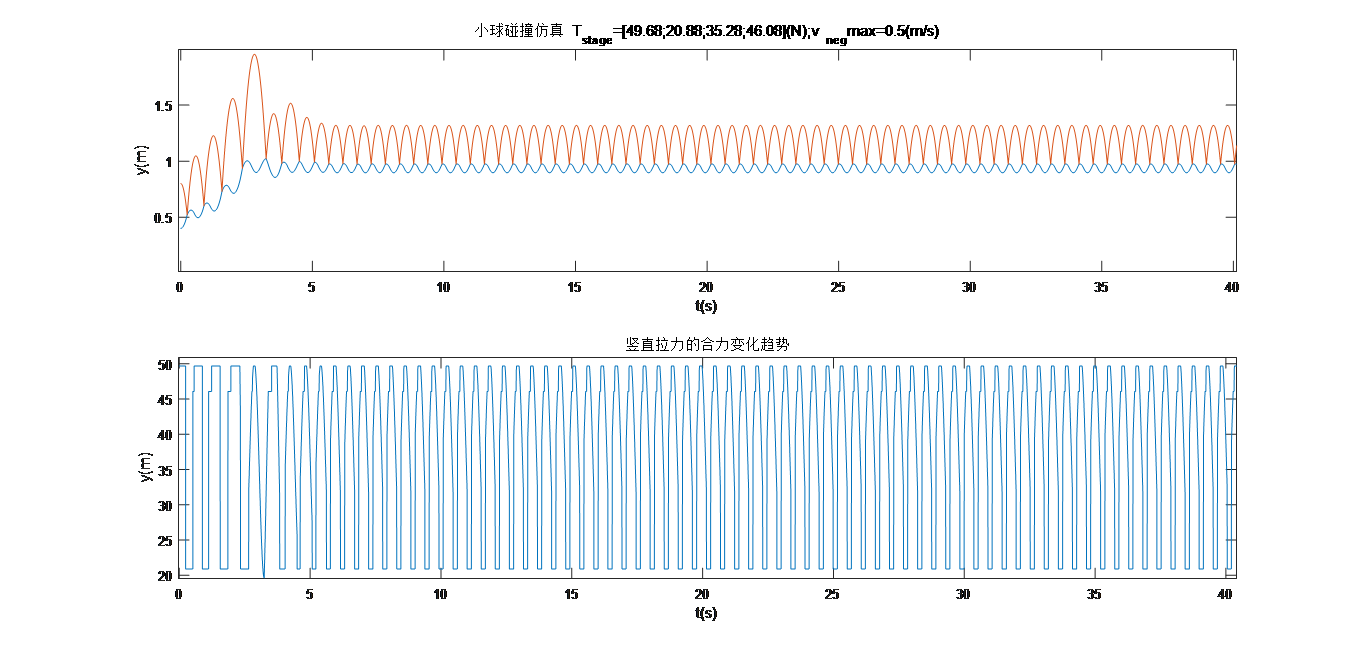
鼓的初始高度对稳定结果没有影响，实验结果如下：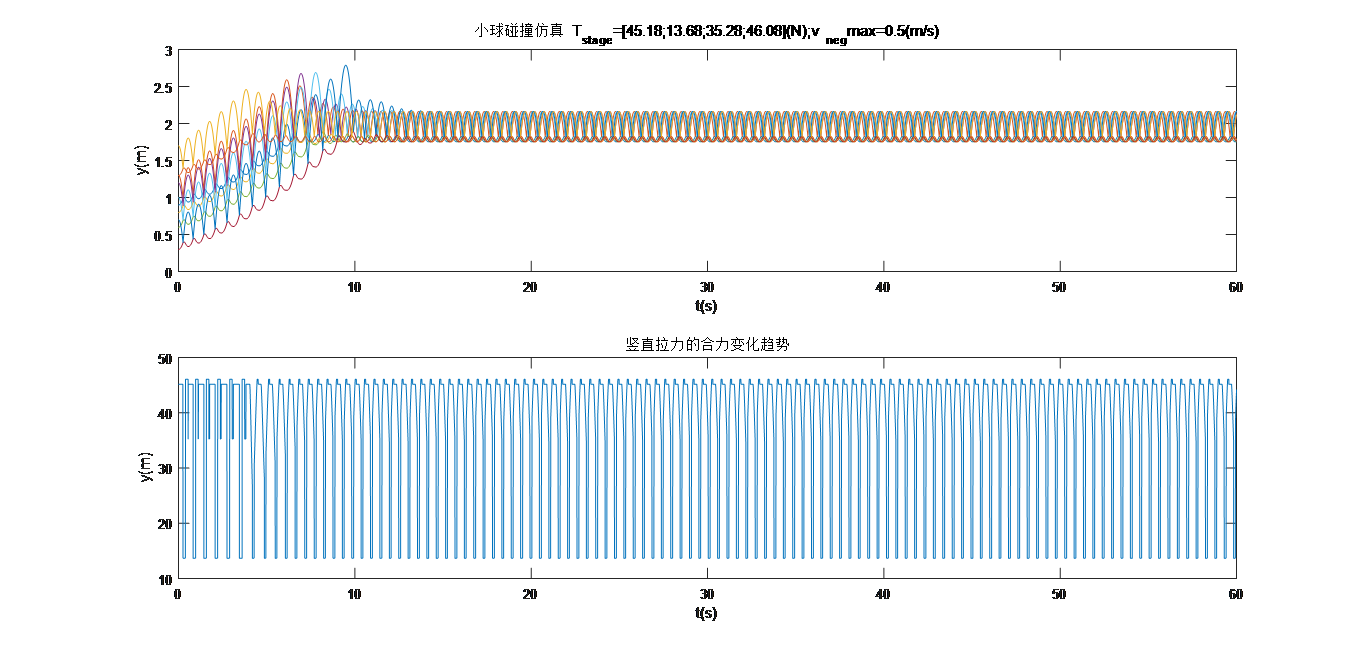

接下来，我们要获取最优值，“最优”是什么？当然是游戏得分多！所以，我们首先要实现：接球数目最多。接下来，我们能接球的时间越长越好。当然，还要考虑一下成员的操作难易度。这个操作难易度定义为$\xi = |\frac{1}{Iter}\sum_{i=1}^{Iter}y_d(i)-y_{conft}|$，其中$y_{conft}$为舒适高度，我们取的0.8，$Iter$为游戏能进行的最大迭代次数，$t_{step}$是迭代步长。

搜索反馈函数的两个lim值和stageI的参考值，求解这个目标规划：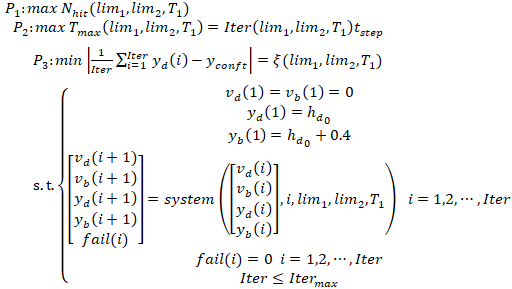

进一步考虑了球的大小，得到最优结果如下：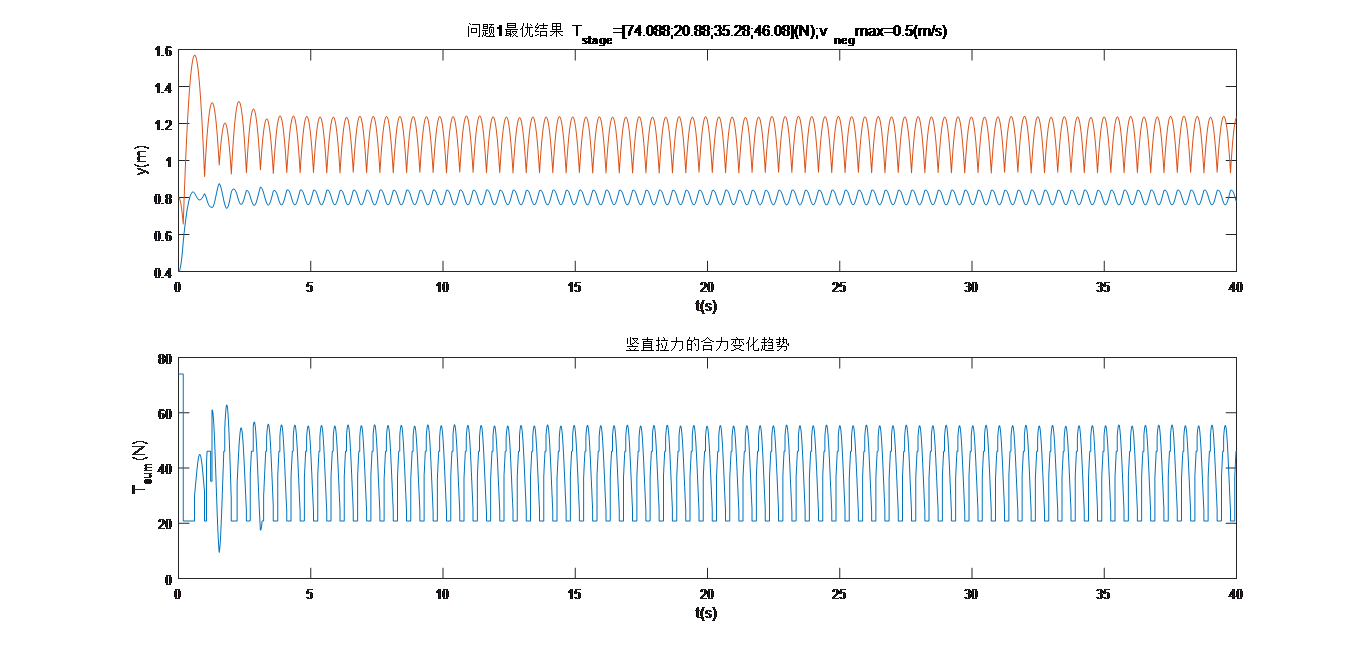

基本符合预期！在迭代时间极限40秒内，击打了80个球！

接下来，将分力分解给每个队员：

设每个队员都有一个舒适施力的值服从正态分布，记为$h_{pull}-N(1.1,0.1^2)$，设N个队员之间夹角为$\gamma=2\pi /N$，
人到鼓边缘的距离$d_{max}=\frac{0.3}{sin(\gamma/2)}-0.2$ (其中0.3=0.6/2,即两人之间距离的一半，0.2为鼓的半径)。
那么，任意时刻，每个人施力夹角为：$\varphi_k(i)=arctan( \frac{h_{pull_k} - y_d(i)}{d_{max}} )$，
每个人施力大小为：$T_k(i)=T_z(i)/(Nsin \varphi_k(i) )$

于是，我们就有了分解之后队员的力与时间的指导规律：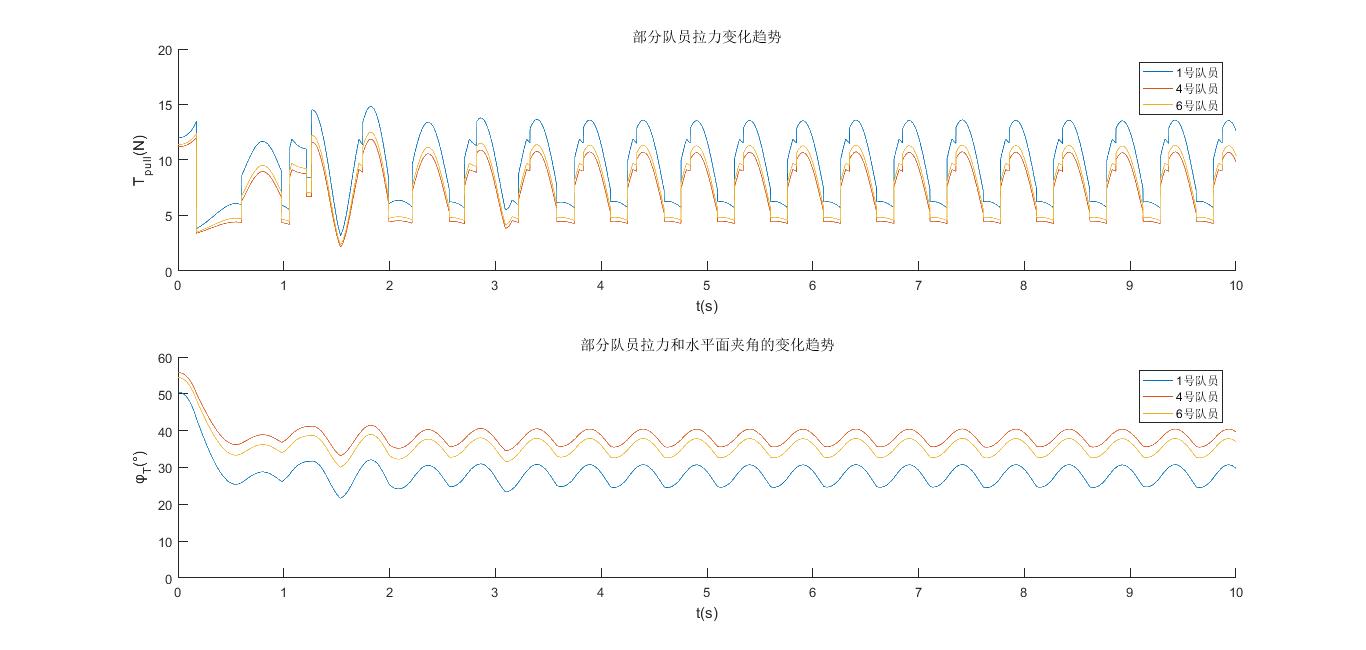

开始向第二问进发！

Second Process: Move to the 3D World

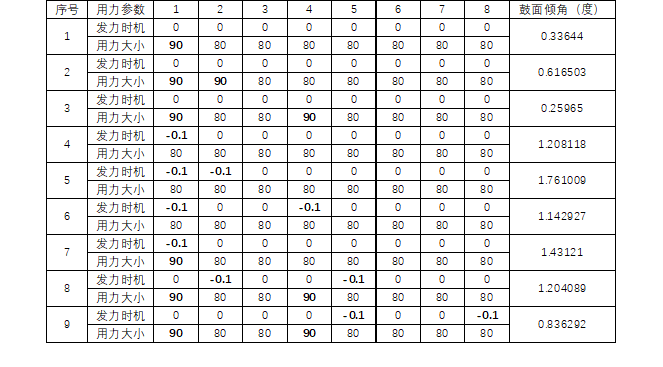
Q2. 在现实情形中，队员发力时机和力度不可能做到精确控制，存在一定误差，于是鼓面可能出现倾斜。试建立模型描述队员的发力时机和力度与某一特定时刻的鼓面倾斜角度的关系。设队员人数为8，绳长为1.7m，鼓面初始时刻是水平静止的，初始位置较绳子水平时下降11 cm，表1中给出了队员们的不同发力时机和力度，求0.1 s时鼓面的倾斜角度。

抱歉，不小心把答案也贴上来了~~（不要紧不要紧~~）

Solution - How to rotate?

第二问其实就是让我们专注建立物理模型了！力都给我们给好了，也没有排球什么事儿，就让鼓运动就是了！关键是：怎么让鼓转起来？

当然是：转动定理！（~~不知道的小伙伴们快快复习大物！~~）

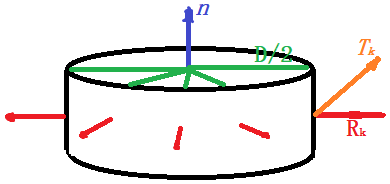
如上图所示：鼓的一些向量属性。$\pmb{R_k}(k=1,2…8)$代表[鼓的中心点]到[鼓面边缘&每个人所在竖直平面交点]的向量，它的长度是$D/2$，D是鼓的直径，方向记为$\pmb{R^o_k}(k=1,2…8)$；$\pmb{T_k}(k=1,2…8)$代表每个人拉力的大小和方向；$\pmb{n}$为鼓的法向量。

另外，我们令：$\pmb{M_k}(k=1,2…8)$为每个人的拉力对鼓造成的力矩，$\pmb{\omega}$为鼓的角速度，$\Delta\theta$为鼓的法向量偏离竖直方向$\pmb{e_z}$的角度，$\pmb{\Delta n}为法向量的瞬时移动量$，$J$为鼓的转动惯量。

转动惯量的计算：将鼓看作圆管状模型，忽略牛皮的质量。制作鼓常用的木材为梧桐木，梧桐木的密度$\rho_{wood}=0.8\times 10^3 kg/m^3$，根据题中给的鼓的尺寸和质量可以求得梧桐木厚度为w=0.0163m；根据转动惯量的定义，鼓相对侧面中轴的转动惯量为：
\begin{equation}
J=\int_{D/2-w}^{D/2} \int_{-h/2}^{h/2} 2 \pi \rho_{wood} (r^2+z^2)rdrdz=0.1517kg·m^2
\end{equation}

那么，我们依然直接列出离散化之后的动力学迭代公式：

转动迭代
$\pmb{M_k}(i)=\frac{D}{2}\pmb{R^o_k}(i)\times\pmb{T_k}(i)(k=1,2…8)$……(每个人造成的分力矩)
$\pmb{M}(i)=\sum^{8}_{k=1}\pmb{M_k}(i)$……(拉力对鼓的合力矩)
$\pmb{\omega}(i+1)=\pmb{\omega}(i)+\pmb{M}(i)\Delta t/J$……(转动定理)
$\pmb{\Delta n}(i)=\pmb{n(i)}\times\pmb{\omega}(i)\Delta t$……(角速度造成的法向量瞬时变化量)
$\pmb{n}(i+1)=\pmb{n}(i)+\pmb{\Delta n}(i)$……(更新法向量)
$\pmb{n}(i+1)=\pmb{n}(i+1)/ | \pmb{n}(i+1) |$……(归一化消除长度误差)
$\pmb{R_k^o}(i+1)=\pmb{R}(i+1)\pmb{R_k^o}(1)$……(按照新的法向量更新鼓的径向,R为旋转矩阵)

平动迭代
$\pmb{f_{d_{air}}}(i) = 0.5 C_d \rho S_d \pmb{v_d}(i) |\pmb{v_d}(i)|$……(鼓的空气阻力)
$m_d \pmb{v_d}(i+1) = (-m_d g\pmb{e_z} + \rho V_d g\pmb{e_z} - \pmb{f_{d_{air}}}(i) + \pmb{\sum T}(i))\Delta t + m_d \pmb{v_d(i)}$……(鼓的速度迭代公式)
$\pmb{r_d}(i+1) = \pmb{r_d}(i) + \pmb{v_d}(i)\Delta t$……(鼓的位置迭代公式)

上面有待确定的量
旋转矩阵$\pmb{R}$的求解: 见博文三维旋转矩阵和刚体旋转(Object Rotation in 3D Space)
$\pmb{\sum T}(i)$: 按照每一时刻表格中给出的力合成为矢量。$\pmb{T}(i)=\sum^{8}_{k=1}\pmb{T_k}(i)$
$\pmb{T_k}(i)$: 方向为$\pmb{T_k^o}(i)=\frac{[cos(2\pi (k-1)/N),sin(2\pi (k-1)/N),tan\varphi_k(i)]}{|[cos(2\pi (k-1)/N),sin(2\pi (k-1)/N),tan\varphi_k(i)]|}$,其中$\varphi_k(i)$的求法在第一问中已给出

至此，我们第二问完全可以求解了。将题目表格中的数据代入，就可以轻松求出任何时刻鼓的位置和角度了！结果如下：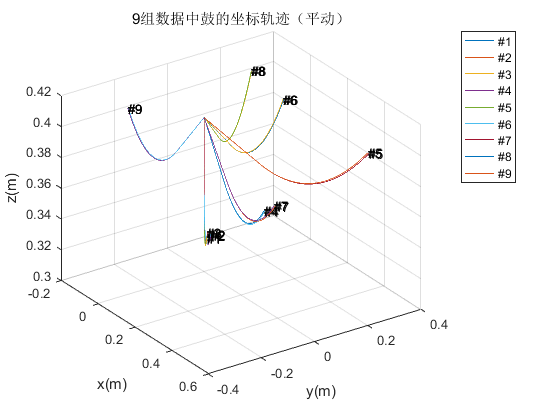

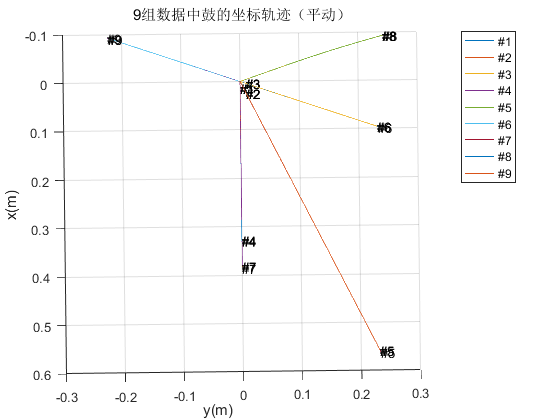
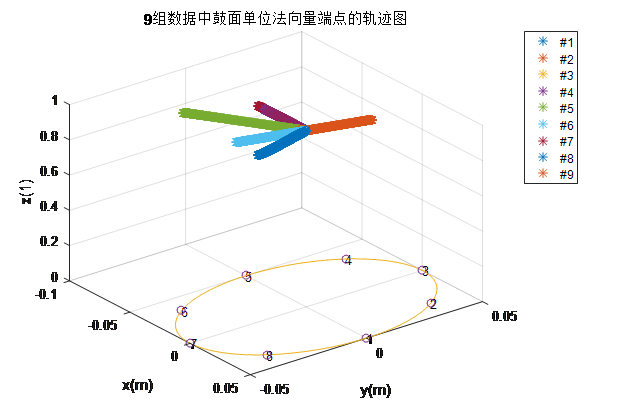
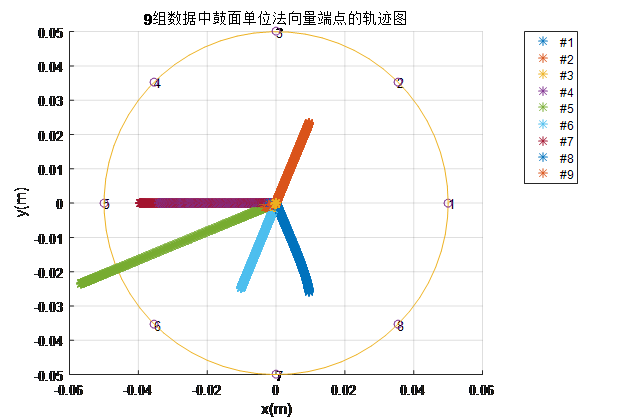
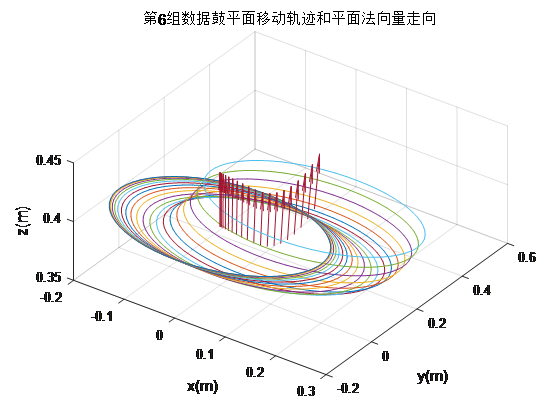
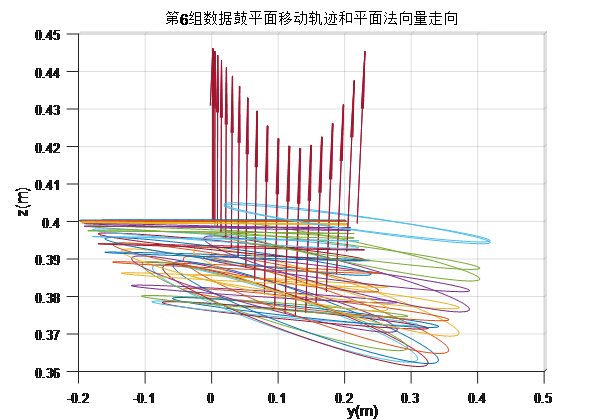
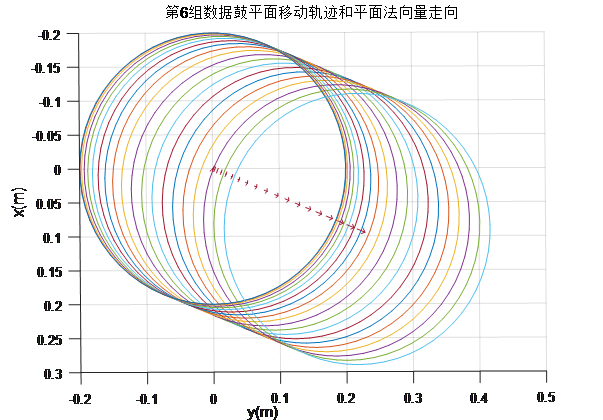
Bonus Experiment

我们还没讨论绳长是否可变和绳子松弛的情况。其实无论如何，影响的都是力$\pmb{T_k}(i)$的$\varphi_k(i)$。假设中，拉力在鼓面的投影一定平行于径向（这样就避免了鼓的水平自转），如果绳长可变，那么可以保证在人的水平位置不变的条件下，拉绳子的手可以竖直运动；如果绳长不可变，即假设人拉绳子总是牵着末端，那么人必定在水平移动。

无论哪种假设，都只是对$\varphi_k(i)$的计算公式产生影响。我们看看$\varphi_k(i)$对倾斜角度（第二问表格里的结果）有什么影响？因为施力时间比较短，所以假设施力过程中$\varphi_k=\varphi$不变。我们得到了这样的结果：

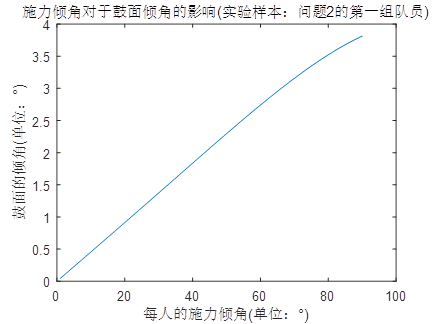
对情形2（施力不均匀）拟合了一下，是一个正弦函数——$\theta = 4^o sin\varphi$
可以发现对结果影响比较小，0.2秒时间内最多影响4°

2019数学建模系列传送门

本文作者： lucainiaoge
本文链接： https://lucainiaoge.github.io.git/2019/09/29/math-modling-2019CUMCM-answer-1/
版权声明： 本作品采用 Creative Commons authorship - noncommercial use - same way sharing 4.0 international license agreement 进行许可。转载请注明出处！

Welcome to my little world